

所以,我已经制作这个井字游戏程序有一段时间了。这是一个基本的井字游戏,但是游戏板是可扩展的。程序快完成了,但是缺少一个小功能。
当游戏板大于4x4时,如果玩家连续获得五个或更多分数,我必须使游戏结束。
F. E.如果游戏板是9x9,游戏必须在玩家或计算机连续获得五分时结束。
(标记=“O”或“X”)。
当有人连续得分等于棋盘大小时,游戏就结束了(如果9x9,你需要连续9分才能获胜)。
我必须在playerHasWon中实现一个功能,我一直很难找到方法。我认为这是一个简单的实现方法,但我还没有找到如何做到这一点。
希望我的解释足够容易理解。这是代码:
package tictac;
import java.util.Scanner;
import java.util.Random;
public class Tictac {
public static final int DRAW = 0; // game ends as a draw
public static final int COMPUTER = 1; // computer wins
public static final int PLAYER = 2; // player wins
public static final char PLAYER_MARK = 'X'; // The "X"
public static final char COMPUTER_MARK = 'O'; // The "O"
public static int size; // size of the board
public static String[][] board; // the board itself
public static int score = 0; // game win score
public static Scanner scan = new Scanner(System.in); // scanner
/**
* Builds the board with the integer size and user input.
*
* Displays game win message and switches play turns.
*
* @param args the command line parameters. Not used.
*/
public static void main(String[] args) {
while (true) {
System.out.println("Select board size");
System.out.print("[int]: ");
try {
size = Integer.parseInt(scan.nextLine());
} catch (Exception e) {
System.out.println("You can't do that.");
continue; // after message, give player new try
}
break;
}
int[] move = {};
board = new String[size][size];
setupBoard();
int i = 1;
loop: // creates the loop
while (true) {
if (i % 2 == 1) {
displayBoard();
move = getMove();
} else {
computerTurn();
}
switch (isGameFinished(move)) {
case PLAYER:
System.err.println("YOU WIN!");
displayBoard();
break loop;
case COMPUTER:
System.err.println("COMPUTER WINS!");
displayBoard();
break loop;
case DRAW:
System.err.println("IT'S A DRAW");
displayBoard();
break loop;
}
i++;
}
}
/**
* Checks for game finish.
*
* @param args command line parameters. Not used.
*
* @return DRAW the game ends as draw.
* @return COMPUTER the game ends as computer win.
* @return PLAYERE the game ends as player win.
*/
private static int isGameFinished(int[] move) {
if (isDraw()) {
return DRAW;
} else if (playerHasWon(board, move,
Character.toString(COMPUTER_MARK))) {
return COMPUTER;
} else if (playerHasWon(board, move,
Character.toString(PLAYER_MARK))) {
return PLAYER;
}
return -1; // can't be 0 || 1 || 2
}
/**
* Checks for win for every direction on the board.
*
* @param board the game board.
* @param move move on the board.
* @param playerMark mark on the board "X" or "O".
* @return the game is won.
*/
public static boolean playerHasWon(String[][] board, int[] move,
String playerMark) { //playermark x || o
// horizontal check
for (int i = 0; i < size; i++) {
if (board[i][0].equals(playerMark)) {
int j;
for (j = 1; j < size; j++) {
if (!board[i][j].equals(playerMark)) {
break;
}
}
if (j == size) {
return true;
}
}
}
// vertical check
for (int i = 0; i < size; i++) {
if (board[0][i].equals(playerMark)) {
int j;
for (j = 1; j < size; j++) {
if (!board[j][i].equals(playerMark)) {
break;
}
}
if (j == size) {
return true;
}
}
}
// diagonals check
int i;
for (i = 0; i < size; i++) {
if (!board[i][i].equals(playerMark)) {
break;
}
}
if (i == size) {
return true;
}
for (i = 0; i < size; i++) {
if (!board[i][(size - 1) - i].equals(playerMark)) {
break;
}
}
return i == size;
}
/**
* Checks for draws.
*
* @return if this game is a draw.
*/
public static boolean isDraw() {
for (int i = 0; i < size; i++) {
for (int j = 0; j < size; j++) {
if (board[i][j] == " ") {
return false;
}
}
}
return true;
}
/**
* Displays the board.
*
*
*/
public static void displayBoard() {
for (int i = 0; i < size; i++) {
for (int j = 0; j < size; j++) {
System.out.printf("[%s]", board[i][j]);
}
System.out.println();
}
}
/**
* Displays the board.
*
*
*/
public static void setupBoard() {
for (int i = 0; i < size; i++) {
for (int j = 0; j < size; j++) {
board[i][j] = " ";
}
}
}
/**
* Takes in user input and sends it to isValidPlay.
*
* @return null.
*/
public static int[] getMove() {
Scanner sc = new Scanner(System.in);
System.out.println("Your turn:");
while (true) {
try {
System.out.printf("ROW: [0-%d]: ", size - 1);
int x = Integer.parseInt(sc.nextLine());
System.out.printf("COL: [0-%d]: ", size - 1);
int y = Integer.parseInt(sc.nextLine());
if (isValidPlay(x, y)) {
board[x][y] = "" + PLAYER_MARK;
return new int[]{x, y};
} else { // if input is unallowed
System.out.println("You can't do that");
continue; // after message, give player new try
}
} catch (Exception e) {
System.out.println("You can't do that.");
}
return null;
}
}
/*
* Randomizes computer's turn, where it inputs the mark 'O'.
*
*
*/
public static void computerTurn() {
Random rgen = new Random(); // Random number generator
while (true) {
int x = (int) (Math.random() * size);
int y = (int) (Math.random() * size);
if (isValidPlay(x, y)) {
board[x][y] = "" + COMPUTER_MARK;
break;
}
}
}
/**
* Checks if a move is possible.
*
* @param inX x-move is out of bounds.
* @param inY y-move is out of bounds.
* @return false
*/
public static boolean isValidPlay(int inX, int inY) {
// Play is out of bounds and thus not valid.
if ((inX >= size) || (inY >= size)) {
return false;
}
// Checks if a play have already been made at the location,
// and the location is thus invalid.
return (board[inX][inY] == " ");
}
}
// End of file
快速查看,检测到问题并提出快速解决方案:
public static boolean checkDiagonal(String markToLook) {
// how many marks are we looking for in row?
int sizeToWin = Math.min(size, 5);
// running down and right
// don't need to iterate rows that can't be the starting point
// of a winning diagonal formation, thus can exlude some with
// row < (size - (sizeToWin - 1))
for (int row = 0; row < (size - (sizeToWin - 1)); row++) {
for (int col = 0; col < size; col++) {
int countOfMarks = 0;
// down and right
for (int i = row; i < size; i++) {
if (board[i][i] == null ? markToLook == null :
board[i][i].equals(markToLook)) {
countOfMarks++;
if (countOfMarks >= sizeToWin) {
return true;
}
}
}
countOfMarks = 0;
// down and left
for (int i = row; i < size; i++) {
if (board[i][size - 1 - i] == null ? markToLook == null :
board[i][size - 1 - i].equals(markToLook)) {
countOfMarks++;
if (countOfMarks >= sizeToWin) {
return true;
}
}
}
}
}
return false;
}
基本上,我们迭代棋盘上的每个可能的起始方块以形成对角线获胜的阵型,并对每个方块分别向左和向右运行check。
我非常匆忙,没有测试太多,但几个小时后会回来改进这个解决方案。似乎有效。
编辑:我发现我以前的解决方案缺乏进一步的测试,我已经更新了上面的代码以按需运行。
首先,我认为playerMark应该是char而不是String。也就是说,让我们寻找答案。“水平”情况是:
// This is the number of marks in a row required to win
// Adjust formula if necessary
final int required = size > 4 ? 5 : 3;
for (int i = 0; i < size; i++) {
int currentScore = 0;
for (j = 0; j < size; j++) {
if (board[i][j].equals(playerMark)) {
currentScore++;
if (currentScore >= required)
return true;
}
else {
currentScore = 0;
}
}
}
}
垂直情况类似。对角线的情况有点棘手,因为现在它需要board[i][i k]作为主对角线,board[i][k-i]作为次要;k和i必须遍历的值可能不明显。这是我的尝试(变量需要作为水平情况):
注意:从这里开始的所有内容都在2015-12-16被完全重写。以前的版本不起作用,算法也没有解释。
在两次失败的尝试后,我决定做我的家庭作业,真正把事情理清楚,而不是在头脑中做所有的事情,认为我可以跟踪所有的变量。结果是这张照片:
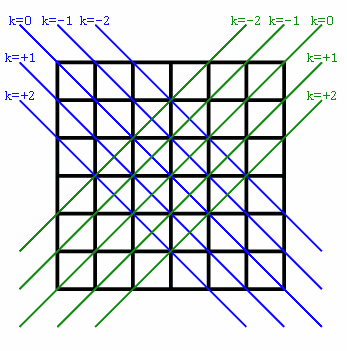
主对角线为蓝色,次对角线为绿色。每个对角线由k值标识,k=0始终是每个集合中最长的对角线。k的值随着对角线向下移动而增长,因此最长对角线上方的对角线为负k,而最长对角线下方的对角线为正k。
两个对角线都成立的东西:
size-abs(k)元素。size-abs(k)小于必需的对角线不需要搜索。这意味着,对于板大小大小和所需长度必需,我们将搜索k的值,从deaded-size到size-必需。请注意,它们具有相同的绝对值,第一个是仅适用于主(蓝色)对角线:
j(列)的值为k i。仅适用于二级(绿色)对角线:
size-1 k-i。如果这不明显,只需选择右上角(k=0, i=0)并注意j=size-1。然后请注意,将1添加到k(保持i恒定)总是将j移动到1右侧(如果从k=0, i=0完成,它会离开棋盘,只要考虑水平线i=0与对角线k=1的交叉点),并且将1添加到i(保持k恒定)总是将j移动到1左侧。重组代码将是://主对角线
for (int k = required - size; k < size - required; k++)
{
int currentScore = 0;
startI = Math.max (0, k);
endI = Math.min (size, size+k);
for (int i = startI, i < endI; i++)
{
if (board[i][k+i].equals (playerMark))
{
currentScore++;
if (currentScore >= required)
return true;
}
else
currentScore = 0;
}
}
// Secondary diagonal
for (int k = required - size; k < size - required; k++)
{
int currentScore = 0;
startI = Math.max (0, k);
endI = Math.min (size, size+k);
for (int i = startI, i < endI; i++)
{
if (board[i][size-1+k-i].equals (playerMark))
{
currentScore++;
if (currentScore >= required)
return true;
}
else
currentScore = 0;
}
}
此时,两种情况下的代码几乎相同,仅更改board[i][j]中的j索引。事实上,两个循环都可以合并,只注意保留两个当前分数变量,一个用于主(蓝色)对角线,另一个用于次(绿色)对角线。