

给定一个凸多边形和一个数字N,我如何找到最小的多边形
例如,假设我有一组点,并为它们计算凸包(绿色)。现在我想找到包含所有点的最小四边形(红色)
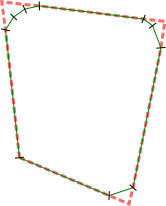
很容易看出,任何其他具有4个角的多边形要么更大,要么无法包含所有点。但是我如何在一般情况下找到这个多边形呢?
编辑:
对于最小的多边形,我指的是覆盖最小面积的多边形,尽管我不确定最小的圆周是否会给出不同的结果。
我添加了另外两个示例图片,不幸的是,它们似乎不适用于其中一个答案中的“删除边缘”方法
一些背景资料:
目标是通过图像识别准确地确定形状。例如,以长方体的照片为例。2D照片中框内的所有点都将包含在6角凸多边形中。然而,由于现实世界的形状没有完美的角,并且相机添加了一些模糊,因此该多边形的边缘将被圆角化。请参阅问题中的附加图像从凸点获取角

你需要在你的问题中定义“最小”的概念。无论你的定义是什么,这个问题在计算几何文献中已经被大量研究过了。关键搜索短语是包含k-gon的最小值:
一般的算法并不简单(尽管最小面积三角形或矩形的算法很简单)。根据你的目标,你可能不得不放弃任何“最小”的数学概念,走向启发式。
While number of edges > N do
remove the shortest edge by replacing its endpoints
with the intersection point of the adjacent edges